5  Timeseries

Temporal data is an area in which Pandas actually far outshines R’s dataframe libraries. Things like resampling and rolling calculations are baked into the dataframe library and work quite well. Fortunately this is also true of Polars!

5.1 Get the data

We’ll download a year’s worth of daily price and volume data for Bitcoin:

from pathlib import Path
from io import StringIO
from datetime import datetime, date
import requests
import polars as pl
import pandas as pd
import matplotlib.pyplot as plt

pl.Config.set_tbl_rows(5)
pd.options.display.max_rows = 5
data_path = Path("../data/ohlcv.pq")


def epoch_ms(dt: datetime) -> int:
    return int(dt.timestamp()) * 1000


if data_path.exists():
    ohlcv_pl = pl.read_parquet(data_path).set_sorted("time")

else:
    start = epoch_ms(datetime(2021, 1, 1))
    end = epoch_ms(datetime(2022, 1, 1))
    url = (
        "https://api.binance.com/api/v3/klines?symbol=BTCUSDT&"
        f"interval=1d&startTime={start}&endTime={end}"
    )
    resp = requests.get(url)
    time_col = "time"
    ohlcv_cols = [
        "open",
        "high",
        "low",
        "close",
        "volume",
    ]
    cols_to_use = [time_col, *ohlcv_cols] 
    cols = cols_to_use + [f"ignore_{i}" for i in range(6)]
    ohlcv_pl = pl.from_records(resp.json(), orient="row", schema=cols).select(
        [
            pl.col(time_col).cast(pl.Datetime).dt.with_time_unit("ms").cast(pl.Date),
            pl.col(ohlcv_cols).cast(pl.Float64),
        ]
    ).set_sorted("time")
    ohlcv_pl.write_parquet(data_path)

ohlcv_pd = ohlcv_pl.with_columns(pl.col("time").cast(pl.Datetime)).to_pandas().set_index("time")

5.2 Filtering

Pandas has special methods for filtering data with a DatetimeIndex. Since Polars doesn’t have an index, we just use .filter. I will admit the Pandas code is more convenient for things like filtering for a specific month:

ohlcv_pl.filter(
    pl.col("time").is_between(
        date(2021, 2, 1),
        date(2021, 3, 1),
        closed="left"
    )
)
shape: (28, 6)
time open high low close volume
date f64 f64 f64 f64 f64
2021-02-01 33092.97 34717.27 32296.16 33526.37 82718.276882
2021-02-02 33517.09 35984.33 33418.0 35466.24 78056.65988
2021-02-03 35472.71 37662.63 35362.38 37618.87 80784.333663
… … … … … …
2021-02-27 46276.88 48394.0 45000.0 46106.43 66060.834292
2021-02-28 46103.67 46638.46 43000.0 45135.66 83055.369042 
ohlcv_pd.loc["2021-02"]
open high low close volume
time
2021-02-01 33092.97 34717.27 32296.16 33526.37 82718.276882
2021-02-02 33517.09 35984.33 33418.00 35466.24 78056.659880
... ... ... ... ... ...
2021-02-27 46276.88 48394.00 45000.00 46106.43 66060.834292
2021-02-28 46103.67 46638.46 43000.00 45135.66 83055.369042

28 rows × 5 columns

5.3 Resampling

Resampling is like a special case of groupby for a time column. You can of course use regular .groupby with a time column, but it won’t be as powerful because it doesn’t understand time like resampling methods do.

There are two kinds of resampling: downsampling and upsampling.

5.3.1 Downsampling

Downsampling moves from a higher time frequency to a lower time frequency. This requires some aggregation or subsetting, since we’re reducing the number of rows in our data.

In Polars we use the .groupby_dynamic method for downsampling (we also use groupby_dynamic when we want to combine resampling with regular groupby logic).

(
    ohlcv_pl
    .group_by_dynamic("time", every="5d")
    .agg(pl.col(pl.Float64).mean())
)
shape: (74, 6)
time open high low close volume
date f64 f64 f64 f64 f64
2020-12-29 29127.665 31450.0 28785.55 30755.01 92088.399186
2021-01-03 33577.028 36008.464 31916.198 35027.986 127574.470245
2021-01-08 38733.61 39914.548 34656.422 37655.352 143777.954392
… … … … … …
2021-12-24 50707.08 51407.656 49540.152 50048.066 29607.160572
2021-12-29 46836.5525 48135.4925 45970.84 46881.2775 31098.406725 
ohlcv_pd.resample("5d").mean()
open high low close volume
time
2021-01-01 31084.316 33127.622 29512.818 32089.662 112416.849570
2021-01-06 38165.310 40396.842 35983.822 39004.538 118750.076685
... ... ... ... ... ...
2021-12-27 48521.240 49475.878 47087.400 47609.528 35886.943710
2022-01-01 46216.930 47954.630 46208.370 47722.650 19604.463250

74 rows × 5 columns

Resampling and performing multiple aggregations to each column:

(
    ohlcv_pl
    .group_by_dynamic("time", every="1w", start_by="friday")
    .agg([
        pl.col(pl.Float64).mean().name.suffix("_mean"),
        pl.col(pl.Float64).sum().name.suffix("_sum")
    ])
)
shape: (53, 11)
time open_mean high_mean low_mean close_mean volume_mean open_sum high_sum low_sum close_sum volume_sum
date f64 f64 f64 f64 f64 f64 f64 f64 f64 f64
2021-01-01 32305.781429 34706.045714 31021.727143 33807.135714 117435.5928 226140.47 242942.32 217152.09 236649.95 822049.149598
2021-01-08 37869.797143 39646.105714 34623.334286 37827.52 135188.296617 265088.58 277522.74 242363.34 264792.64 946318.076319
2021-01-15 36527.891429 37412.2 33961.551429 35343.847143 94212.715129 255695.24 261885.4 237730.86 247406.93 659489.005903
… … … … … … … … … … …
2021-12-24 49649.114286 50439.622857 48528.25 49117.98 31126.709793 347543.8 353077.36 339697.75 343825.86 217886.96855
2021-12-31 46668.905 48251.445 45943.185 46969.79 27271.230605 93337.81 96502.89 91886.37 93939.58 54542.46121 
ohlcv_pd.resample("W-Fri", closed="left", label="left").agg(['mean', 'sum'])
open high low close volume
mean sum mean sum mean sum mean sum mean sum
time
2021-01-01 32305.781429 226140.47 34706.045714 242942.32 31021.727143 217152.09 33807.135714 236649.95 117435.592800 822049.149598
2021-01-08 37869.797143 265088.58 39646.105714 277522.74 34623.334286 242363.34 37827.520000 264792.64 135188.296617 946318.076319
... ... ... ... ... ... ... ... ... ... ...
2021-12-24 49649.114286 347543.80 50439.622857 353077.36 48528.250000 339697.75 49117.980000 343825.86 31126.709793 217886.968550
2021-12-31 46668.905000 93337.81 48251.445000 96502.89 45943.185000 91886.37 46969.790000 93939.58 27271.230605 54542.461210

53 rows × 10 columns

5.3.2 Upsampling

Upsampling moves in the opposite direction, from low-frequency data to high frequency data. Since we can’t create new data by magic, upsampling defaults to filling the new rows with nulls (which we could then interpolate, perhaps). In Polars we have a special upsample method for this, while Pandas reuses its resample method.

ohlcv_pl.upsample("time", every="6h")
shape: (1_461, 6)
time open high low close volume
date f64 f64 f64 f64 f64
2021-01-01 28923.63 29600.0 28624.57 29331.69 54182.925011
2021-01-01 null null null null null
2021-01-01 null null null null null
… … … … … …
2021-12-31 null null null null null
2022-01-01 46216.93 47954.63 46208.37 47722.65 19604.46325 
ohlcv_pd.resample("6h").mean()
open high low close volume
time
2021-01-01 00:00:00 28923.63 29600.00 28624.57 29331.69 54182.925011
2021-01-01 06:00:00 NaN NaN NaN NaN NaN
... ... ... ... ... ...
2021-12-31 18:00:00 NaN NaN NaN NaN NaN
2022-01-01 00:00:00 46216.93 47954.63 46208.37 47722.65 19604.463250

1461 rows × 5 columns

5.4 Rolling / Expanding / EW

Polars supports all three of these but they’re not quite as powerful as in Pandas, since they don’t have as many different methods. The expanding support is more limited again, though there are workarounds for this (see below):

close = pl.col("close")
ohlcv_pl.select(
    [
        pl.col("time"),
        close.alias("Raw"),
        close.rolling_mean(28).alias("28D MA"),
        close.alias("Expanding Average").cum_sum() / (close.cum_count() + 1),
        close.ewm_mean(alpha=0.03).alias("EWMA($\\alpha=.03$)"),
    ]
).to_pandas().set_index("time").plot()

plt.ylabel("Close ($)")
Text(0, 0.5, 'Close ($)')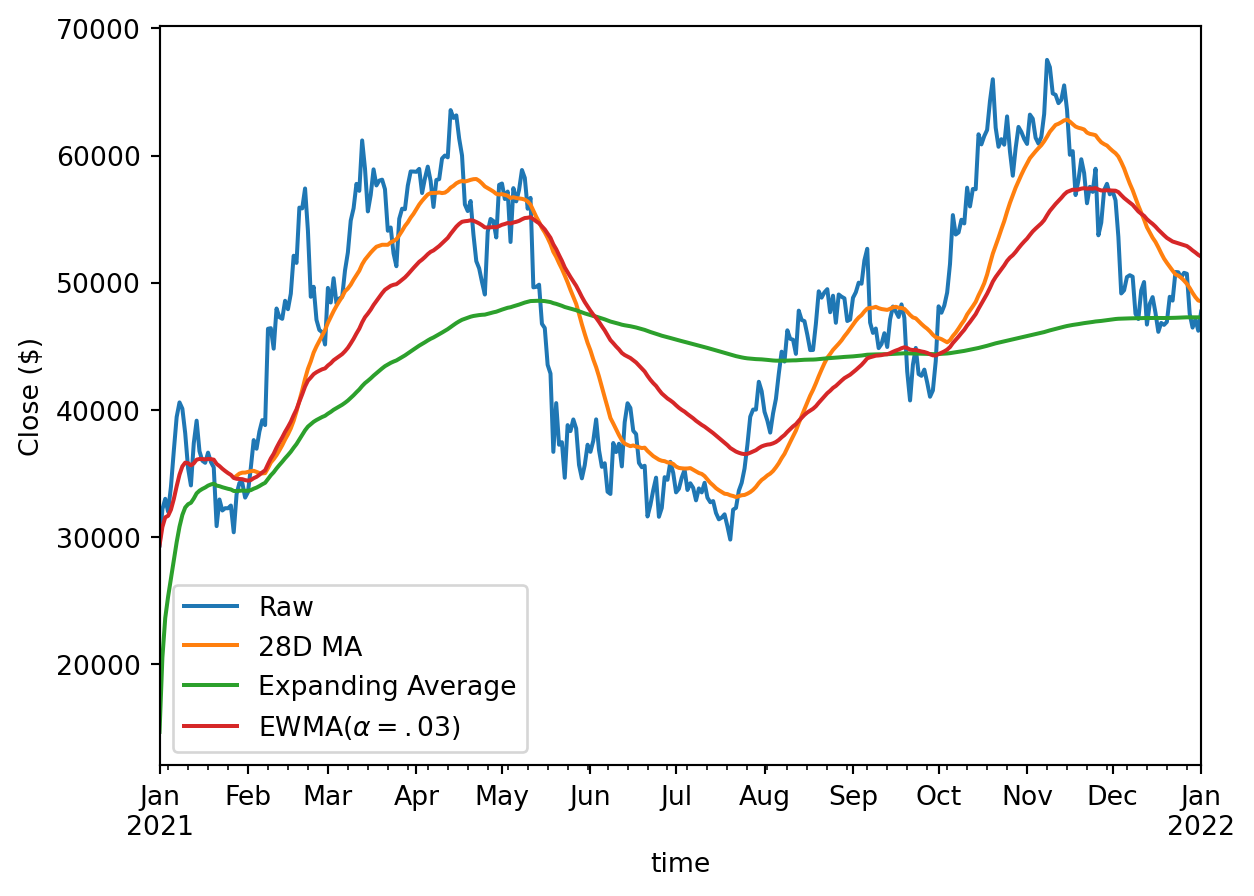

ohlcv_pd["close"].plot(label="Raw")
ohlcv_pd["close"].rolling(28).mean().plot(label="28D MA")
ohlcv_pd["close"].expanding().mean().plot(label="Expanding Average")
ohlcv_pd["close"].ewm(alpha=0.03).mean().plot(label="EWMA($\\alpha=.03$)")

plt.legend(bbox_to_anchor=(0.63, 0.27))
plt.ylabel("Close ($)")
Text(0, 0.5, 'Close ($)')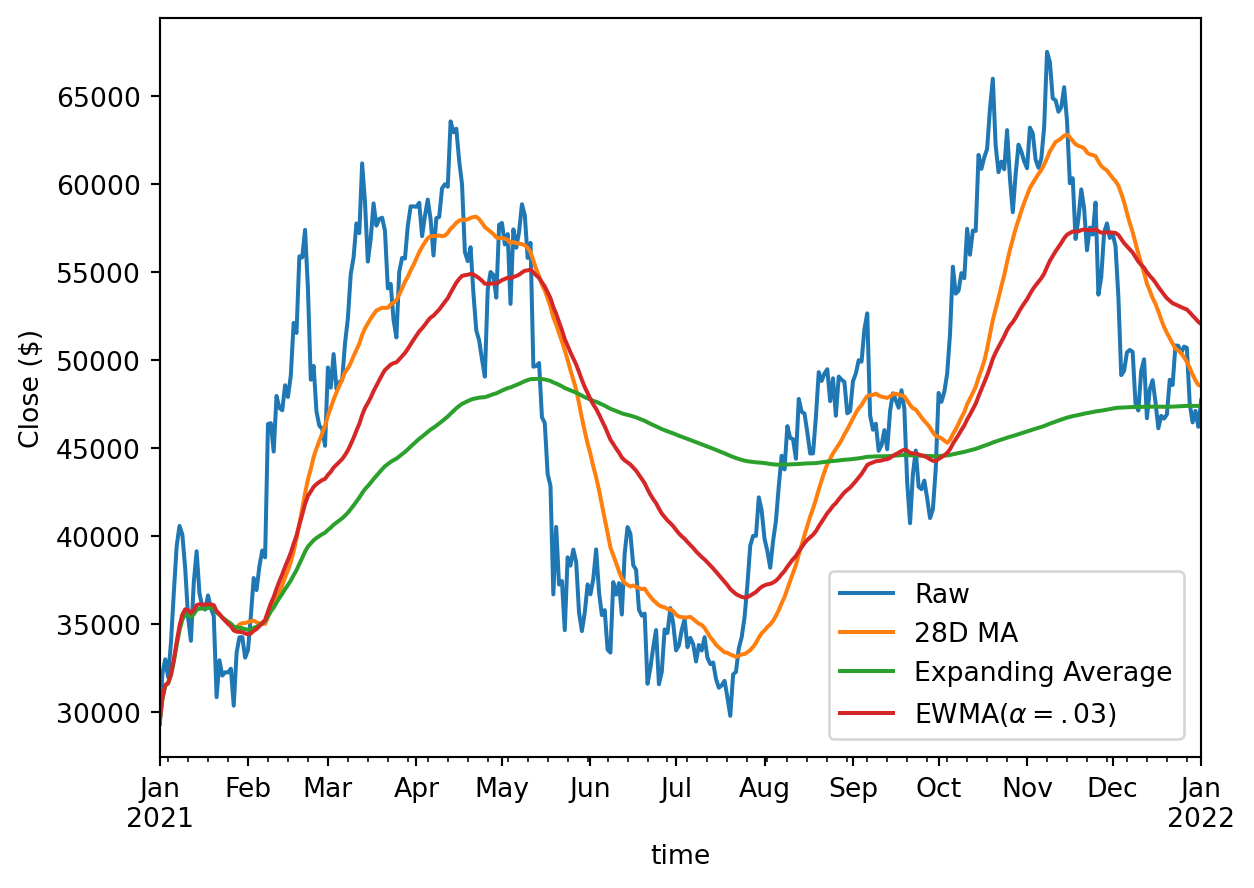

Polars doesn’t have an expanding_mean yet so we make do by combining cumsum and cumcount.

5.4.1 Combining rolling aggregations

mean_std_pl = ohlcv_pl.select(
    [
        "time",
        pl.col("close").rolling_mean(30, center=True).alias("mean"),
        pl.col("close").rolling_std(30, center=True).alias("std"),
    ]
)
ax = mean_std_pl.to_pandas().set_index("time")["mean"].plot()
ax.fill_between(
    mean_std_pl["time"].to_numpy(),
    mean_std_pl["mean"] - mean_std_pl["std"],
    mean_std_pl["mean"] + mean_std_pl["std"],
    alpha=0.25,
)
plt.tight_layout()
plt.ylabel("Close ($)")
Text(26.83333333333334, 0.5, 'Close ($)')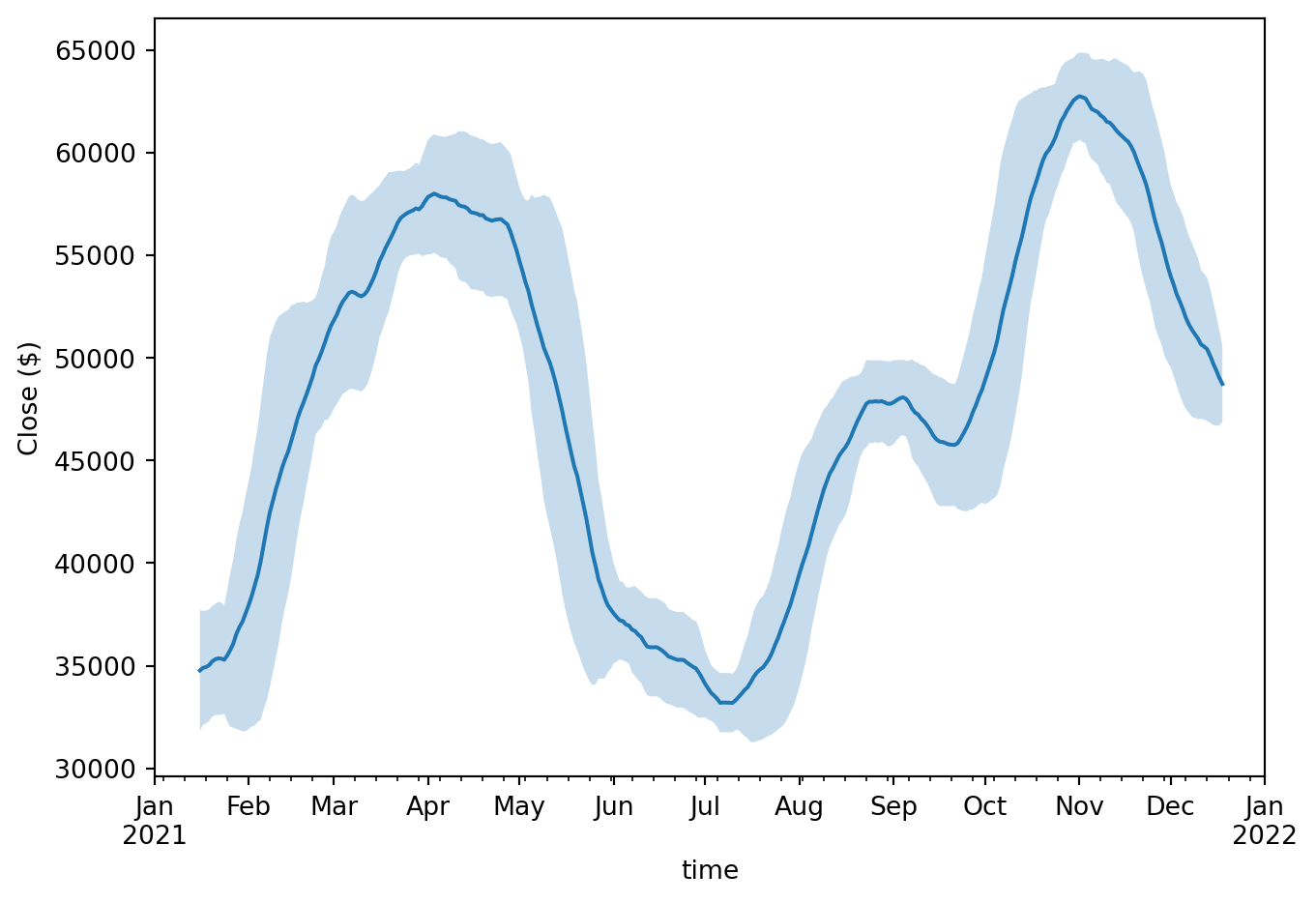

roll_pd = ohlcv_pd["close"].rolling(30, center=True)
mean_std_pd = roll_pd.agg(["mean", "std"])
ax = mean_std_pd["mean"].plot()
ax.fill_between(
    mean_std_pd.index,
    mean_std_pd["mean"] - mean_std_pd["std"],
    mean_std_pd["mean"] + mean_std_pd["std"],
    alpha=0.25,
)
plt.tight_layout()
plt.ylabel("Close ($)")
Text(26.83333333333334, 0.5, 'Close ($)')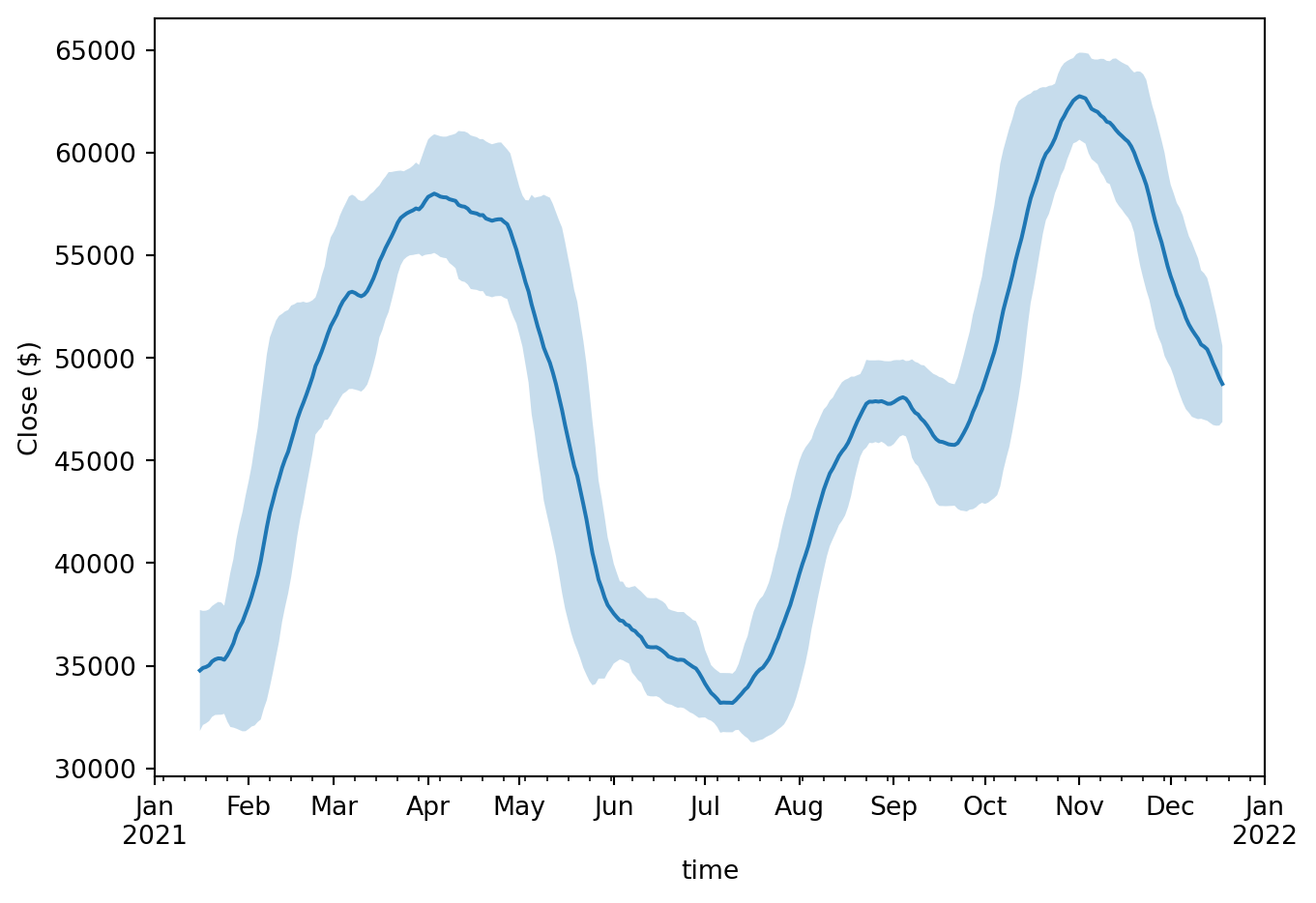

5.5 Grab Bag

5.5.1 Offsets

Pandas has two similar objects for datetime arithmetic: DateOffset which respects calendar arithmetic, and Timedelta which respects absolute time arithmetic. DateOffset understands things like daylight savings time, and can work with holidays too.

Polars just has a Duration type which is like Pandas Timedelta.

ohlcv_pl.select(pl.col("time") + pl.duration(days=80))
shape: (366, 1)
time
date
2021-03-22
2021-03-23
2021-03-24
…
2022-03-21
2022-03-22 
ohlcv_pd.index + pd.Timedelta(80, "D")
DatetimeIndex(['2021-03-22', '2021-03-23', '2021-03-24', '2021-03-25',
               '2021-03-26', '2021-03-27', '2021-03-28', '2021-03-29',
               '2021-03-30', '2021-03-31',
               ...
               '2022-03-13', '2022-03-14', '2022-03-15', '2022-03-16',
               '2022-03-17', '2022-03-18', '2022-03-19', '2022-03-20',
               '2022-03-21', '2022-03-22'],
              dtype='datetime64[ns]', name='time', length=366, freq=None)
ohlcv_pd.index + pd.DateOffset(months=3, days=-10)
DatetimeIndex(['2021-03-22', '2021-03-23', '2021-03-24', '2021-03-25',
               '2021-03-26', '2021-03-27', '2021-03-28', '2021-03-29',
               '2021-03-30', '2021-03-31',
               ...
               '2022-03-13', '2022-03-14', '2022-03-15', '2022-03-16',
               '2022-03-17', '2022-03-18', '2022-03-19', '2022-03-20',
               '2022-03-21', '2022-03-22'],
              dtype='datetime64[us]', name='time', length=366, freq=None)

5.5.2 Holiday calendars

Not many people know this, but Pandas can do some quite powerful stuff with Holiday Calendars. There is an open issue to add this functionality to Polars.

5.5.3 Timezones

Suppose we know that our timestamps are UTC, and we want to see what time it was in US/Eastern:

(
    ohlcv_pl
    .with_columns(
        pl.col("time")
        .cast(pl.Datetime)
        .dt.replace_time_zone("UTC")
        .dt.convert_time_zone("US/Eastern")
    )
)
shape: (366, 6)
time open high low close volume
datetime[μs, US/Eastern] f64 f64 f64 f64 f64
2020-12-31 19:00:00 EST 28923.63 29600.0 28624.57 29331.69 54182.925011
2021-01-01 19:00:00 EST 29331.7 33300.0 28946.53 32178.33 129993.873362
2021-01-02 19:00:00 EST 32176.45 34778.11 31962.99 33000.05 120957.56675
… … … … … …
2021-12-30 19:00:00 EST 47120.88 48548.26 45678.0 46216.93 34937.99796
2021-12-31 19:00:00 EST 46216.93 47954.63 46208.37 47722.65 19604.46325 
(
    ohlcv_pd
    .tz_localize('UTC')
    .tz_convert('US/Eastern')
)
open high low close volume
time
2020-12-31 19:00:00-05:00 28923.63 29600.00 28624.57 29331.69 54182.925011
2021-01-01 19:00:00-05:00 29331.70 33300.00 28946.53 32178.33 129993.873362
... ... ... ... ... ...
2021-12-30 19:00:00-05:00 47120.88 48548.26 45678.00 46216.93 34937.997960
2021-12-31 19:00:00-05:00 46216.93 47954.63 46208.37 47722.65 19604.463250

366 rows × 5 columns

5.6 Conclusion

Polars has really good time series support, though expanding aggregations and holiday calendars are niches in which it is lacking. Pandas DateTimeIndexes are quite cool too, even if they do bring some pain.